
Digital evolution is a form of evolutionary computation in which self-replicating computer programs—digital organisms—evolve within a user-defined computational environment. Avida is the most widely used software platform for research in digital evolution. It satisfies the three essential requirements for evolution to occur: replication, heritable variation, and differential fitness. The latter arises through competition for the limited resources of memory space and central processing unit (CPU) time.
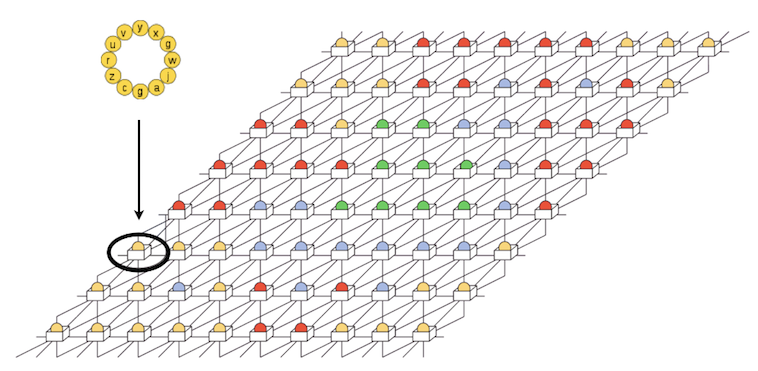
A digital organism in Avida consists of a sequence of instructions—its genome or genotype—and a virtual CPU, which executes these instructions. Some of these instructions are involved in copying an organism’s genome, which is the only way the organism can pass on its genetic material to future generations. To reproduce, a digital organism must copy its genome instruction by instruction into a new region of memory through a process that may lead to errors (i.e., mutations). A mutation occurs when an instruction is copied incorrectly, and is instead replaced in the offspring genome by an instruction chosen at random (with a uniform distribution) from a set of possible instructions.
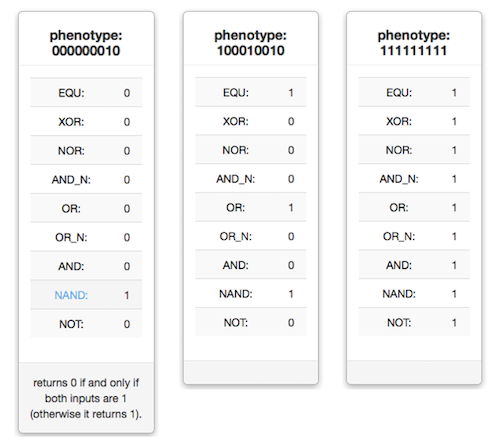
Some instructions are required for replication (i.e., viability), whereas others are required to complete computational operations (such as addition, multiplications, and bit-shifts), and are executed on binary numbers taken from the environment through input-output instructions. When the output of processing these numbers equals the result of a specific Boolean logic operation, the digital organism is said to have a functional trait represented by that logic operation.

An organism can be rewarded for having a functional trait with virtual CPU-cycles, which speeds up its execution of instructions. These rewards create an additional selective pressure (besides streamlining replication) which favours those organisms with mutations that have produced sequences of instructions in their genomes that encode functional traits. Organisms that are more successful—those that replicate faster—are more likely to spread through a population.
The genome of a digital organism.
The genome of a digital organism is a circular sequence of instructions taken from a 26-instruction alphabet. It comprises instructions for copying (e.g., v, w, x) as well as for completing computational operations (such as additions, subtractions, and bit-shifts), which are executed on binary numbers taken from the environment. The default environment provides the organism with new, random input strings every time an input-output instruction (y) is executed.
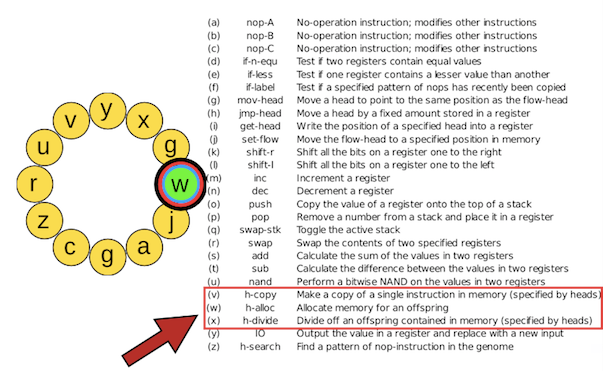
The genome of a digital organism can harbor one or several input-output instructions (y) that can be executed either only once or many times during the time it takes to generate an offspring. This means that the organism can take input numbers from the environment more than once before replicating and can compute the result of more than one logic operation (see below). Only one instruction from the instruction set is itself a logic operator (u).
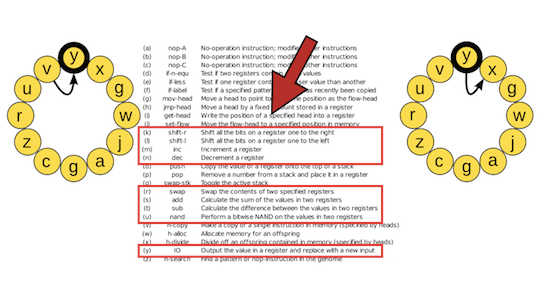
This is the nand (not-and) instruction, which must be executed in coordination with input-output instructions (y) to perform the NAND logic operation. The nand instruction reads in the contents of the BX and CX registers and performs a bitwise NAND operation on them (i.e., it returns 0 if and only if both inputs at the corresponding bit positions are 1, otherwise it returns 1).
The result of this operation is placed in the BX register. The input-output instruction (y) takes the contents of the BX register and outputs it, checking it for any logic operations that may have been performed. It will then place a new input into BX. All other logic operations must be performed using one or more nand instructions in combination with input-output (y) instructions.
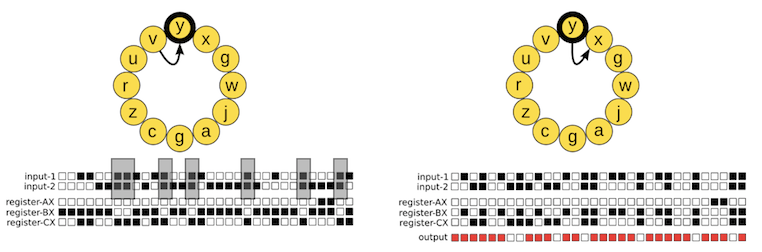
y; highlighted in black). Left, the state of the input buffers and registers before executing the input-output instruction (the arrow points toward the next instruction to be executed). Right, the state of the input buffers, registers, and the output after executing the input-output instruction. The input-output instruction outputs the number stored in the BX register, checking for any logic operation that may have been performed on the two binary numbers previously stored in the input buffers. In this example, the output is the result of applying the logic operation NAND: for each bit pair, the result is 0 (white box) if and only if the two bits are 1, and 1 otherwise (red box). Then, the input-output instruction places a new random binary number into the BX register (a number that is also stored in the input-1 buffer after moving the number previously stored there to the input-2 buffer). Figure taken from our paper).The phenotype of a digital organism.
Phenotypes are defined by the combination of the following 9 Boolean logic operations that organisms can perform on 32-bit one- and two-input numbers: NOT, which returns 1 at a bit position if the input is 0 at that bit position, and 0 if the input is 1; NAND, which returns 0 if and only if both inputs at the corresponding bit positions are 1 (otherwise it returns 1); AND, which returns 1 if and only if both inputs are 1 (otherwise it returns 0); OR_N (or-not), which returns 1 if for each input bit pair one input bit is 1 or the other is 0 (otherwise it returns 0); OR, which returns 1 if either the first input, the second input, or both are 1 (otherwise it returns 0); AND_N (and-not), which only returns 1 if for each bit pair one input is 1 and the other input is 0 (otherwise it returns 0); NOR (not-or), which returns 1 only if both inputs are 0 (otherwise it returns 0); XOR (exclusive OR), which returns 1 if one but not both of the inputs are 1 (otherwise it returns 0); EQU (equals), which returns 1 if both bits are identical, and 0 if they are different.
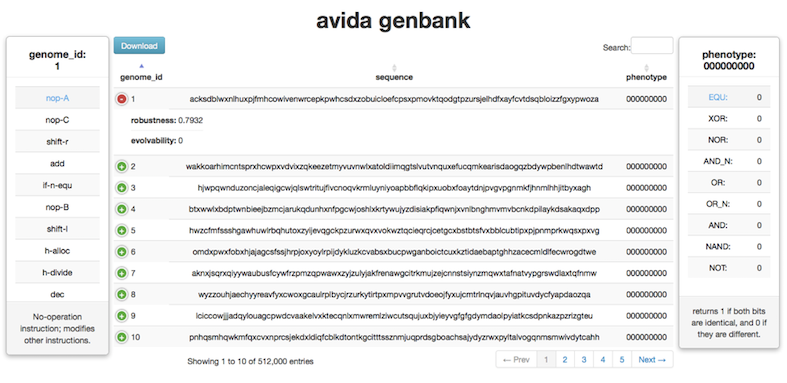
You can explore a database of 512,000 organism's genomes and the phenotypes they encode in a single environment here.
Charles Ofria and Claus O. Wilke explain here the general principles on which Avida is built, as well as its main components and their interactions.

